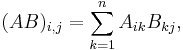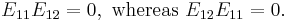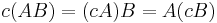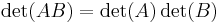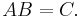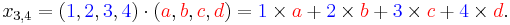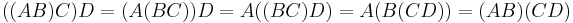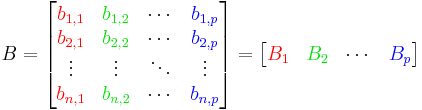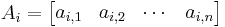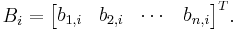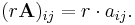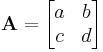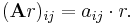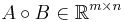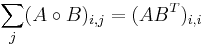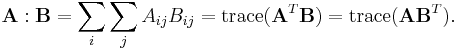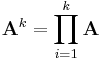Matrix multiplication

In mathematics, matrix multiplication is the operation of multiplying a matrix with either a scalar or another matrix. This article gives an overview of the various types of matrix multiplication.

1 Matrix product
2 Algorithms for efficient matrix multiplication
3 Scalar multiplication
4 Hadamard product
5 Kronecker product
6 Frobenius inner product
7 Powers of matrices
- 7.1 Powers of diagonal matrices
8 See also
9 Notes
10 References
11 External links

Matrix product

The matrix product is the most commonly used type of product of matrices. Matrices offer a concise way of representing linear transformations between vector spaces, and matrix multiplication corresponds to the composition of linear transformations. The matrix product of two matrices can be defined when their entries belong to the same ring, and hence can be added and multiplied, and, additionally, the number of the columns of the first matrix matches the number of the rows of the second matrix. The product of an m×p matrix A with an p×n matrix B is an m×n matrix denoted AB whose entries are

$(AB)_{i,j} = \sum_{k=1}^n A_{ik}B_{kj},$

where 1 ≤ i ≤ m is the row index and 1 ≤ j ≤ n is the column index. This definition can be restated by postulating that the matrix product is left and right distributive and the matrix units are multiplied according to the following rule:

$E_{ik} E_{lj} = \delta_{kl} E_{ij},$

where the first factor is the m×n matrix with 1 at the intersection of the ith row and the kth column and zeros elsewhere and the second factor is the p×n matrix with 1 at the intersection of the lth row and the jth column and zeros elsewhere.

Properties

In general, matrix multiplication is not commutative. More precisely, AB and BA need not be simultaneously defined; if they are, they may have different dimensions; and even if A and B are square matrices of the same order n, so that AB and BA are also square matrices of order n, if n is greater or equal than 2, AB need not be equal to BA. For example,

$E_{11}E_{12}=0, \text{ whereas } E_{12}E_{11}=0.$

However, if A and B are both diagonal square matrices of the same order then AB = BA.

Matrix multiplication is associative:

$\ {A} ( {B C} ) = ( {A B} ) {C}.$

Matrix multiplication is distributive over matrix addition:

$\ A ({B} + {C} ) = {A B} + {AC}, \quad ({A} + {B} ){C} = {A C} + {B C},$

provided that the expression in either side of each identity is defined.

For matrices with entries in a field, the matrix product is compatible with scalar multiplication:

$\ c(AB) = (cA)B = A(cB)$

where c is a scalar.

If A and B are both nxn matrices with entries in a field then the determinant of their product is the product of their determinants:

$\;\!\det(AB) = \det(A)\det(B)$

In particular, the determinants of AB and BA coincide.

Let U, V, and W be vector spaces over the same field with certain bases, S: V → W and T: U → V be linear transformations and ST: U → W be their composition. Suppose that A, B, and C are the matrices of T, S, and ST with respect to the given bases. Then

$AB=C.$

Thus the matrix of the composition (or the product) of linear transformations is the product of their matrices with respect to the given bases.

Illustration

The figure to the right illustrates the product of two matrices A and B, showing how each intersection in the product matrix corresponds to a row of A and a column of B. The size of the output matrix is always the largest possible, i.e. for each row of A and for each column of B there are always corresponding intersections in the product matrix. The product matrix AB consists of all combinations of dot products of rows of A and columns of B.

The values at the intersections marked with circles are:

$\begin{align} {\color{Red}x_{1,2}} &= (a_{1,1}, a_{1,2})\cdot(b_{1,2}, b_{2,2}) \\ &= a_{1, 1}b_{1,2} + a_{1,2}b_{2, 2} \\ {\color{Blue}x_{3,3}} &= (a_{3,1}, a_{3, 2})\cdot(b_{1, 3}, b_{2, 3}) \\ &= a_{3, 1}b_{1,3} + a_{3,2}b_{2, 3}. \end{align}$

In general, the matrix product is non-commutative. For example,

$\overset{3\times 4 \text{ matrix}}{\begin{bmatrix} \cdot & \cdot & \cdot & \cdot \\ \cdot & \cdot & \cdot & \cdot \\ \color{Blue} 1 & \color{Blue} 2 & \color{Blue} 3 & \color{Blue} 4 \\ \end{bmatrix}} \overset{4\times 5\text{ matrix}}{\begin{bmatrix} \cdot & \cdot & \cdot & \color{Red}a & \cdot \\ \cdot & \cdot & \cdot & \color{Red}b & \cdot \\ \cdot & \cdot & \cdot & \color{Red}c & \cdot \\ \cdot & \cdot & \cdot & \color{Red}d & \cdot \\ \end{bmatrix}} = \overset{3\times 5\text{ matrix}}{ \begin{bmatrix} \cdot & \cdot & \cdot & \cdot & \cdot \\ \cdot & \cdot & \cdot & \cdot & \cdot \\ \cdot & \cdot & \cdot & x_{3,4} & \cdot \\ \end{bmatrix}}$

The element $x_{3,4}$ of the above matrix product is computed as follows

$x_{3,4} = ({\color{Blue}1}, {\color{Blue}2}, {\color{Blue}3}, {\color{Blue}4})\cdot ({\color{Red}a}, {\color{Red}b}, {\color{Red}c}, {\color{Red}d}) = {\color{Blue} 1}\times{\color{Red} a} +{\color{Blue} 2}\times{\color{Red} b} +{\color{Blue} 3}\times{\color{Red} c} +{\color{Blue} 4}\times{\color{Red} d}.$

The first coordinate in matrix notation denotes the row and the second the column; this order is used both in indexing and in giving the dimensions. The element $x_{{\color{Blue}i}{\color{Red}j}}$ at the intersection of row $i$ and column $j$ of the product matrix is the dot product (or scalar product) of row $i$ of the first matrix and column $j$ of the second matrix. This explains why the width and the height of the matrices being multiplied must match: otherwise the dot product is not defined.

Product of several matrices

Matrix product can be extended to the case of several matrices, provided that their dimensions match, and it is associative, i.e. the result does not depend on the way the factors are grouped together. If A, B, C, and D are, respectively, an m×p, p×q, q×r, and r×n matrices, then there are 5 ways of grouping them without changing their order, and

$((AB)C)D=(A(BC))D=A((BC)D)=A(B(CD))=(AB)(CD)$

is an m×n matrix denoted ABCD.

Alternative descriptions

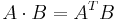The Euclidean inner product and outer product are the simplest special cases of the matrix product. The inner product of two column vectors $A$ and $B$ is $A\cdot B = A^TB$ , where T denotes the matrix transpose. More explicitly,

$A\cdot B = A^TB = \begin{bmatrix}a_1 & a_2 & \cdots & a_n\end{bmatrix} \begin{bmatrix}b_1 \\ b_2 \\ \vdots \\ b_n\end{bmatrix} = \begin{bmatrix} a_1b_1+a_2b_2+\cdots+a_nb_n \end{bmatrix}.$

The outer product is 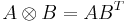$A\otimes B = AB^T$ , where

$AB^T = \begin{bmatrix}a_1 \\ a_2 \\ \vdots \\ a_n\end{bmatrix} \begin{bmatrix}b_1 & b_2 & \cdots & b_n\end{bmatrix} = \begin{bmatrix} a_1 b_1 & a_1 b_2 & \cdots & a_1 b_n \\ a_2 b_1 & a_2 b_2 & \cdots & a_2 b_n \\ \vdots & \vdots & \ddots & \vdots \\ a_n b_1 & a_n b_2 & \cdots & a_n b_n \\ \end{bmatrix}.$

Matrix multiplication can be viewed in terms of these two operations by considering the effect of the matrix product on block matrices.

Suppose that the first factor, A, is decomposed into its rows, which are row vectors and the second factor, B, is decomposed into its columns, which are column vectors:

${A} = \begin{bmatrix} {\color{Red} a_{1,1}} & {\color{Red}a_{1, 2}} & \cdots & {\color{Red} a_{1, n}} \\ {\color{ForestGreen} a_{2,1}} & {\color{ForestGreen} a_{2, 2}} & \cdots & {\color{ForestGreen} a_{2, n}} \\ \vdots & \vdots & \ddots & \vdots \\ {\color{Blue} a_{m, 1}} & {\color{Blue} a_{m, 2}} & \cdots & {\color{Blue} a_{m, n}} \end{bmatrix} = \begin{bmatrix} {\color{Red} A_1} \\ {\color{ForestGreen} A_2} \\ \vdots \\ {\color{Blue} A_m} \end{bmatrix}$

${B} = \begin{bmatrix} {\color{Red}b_{1,1}} & {\color{ForestGreen}b_{1, 2}} & \cdots & {\color{Blue}b_{1, p}} \\ {\color{Red}b_{2,1}} & {\color{ForestGreen}b_{2, 2}} & \cdots & {\color{Blue}b_{2, p}} \\ \vdots & \vdots & \ddots & \vdots \\ {\color{Red}b_{n, 1}} & {\color{ForestGreen}b_{n, 2}} & \cdots & {\color{Blue}b_{n, p}} \end{bmatrix} = \begin{bmatrix} {\color{Red} B_1} & {\color{ForestGreen} B_2} & \cdots & {\color{Blue} B_p} \end{bmatrix}$

where

$A_i = \begin{bmatrix}a_{i, 1} & a_{i, 2} & \cdots & a_{i, n} \end{bmatrix}$

$B_i = \begin{bmatrix}b_{1, i} & b_{2, i} & \cdots & b_{n, i}\end{bmatrix}^T.$

The method in the introduction was:

${AB} = \begin{bmatrix} A_1 \\ A_2 \\ \vdots \\ A_m \end{bmatrix} \begin{bmatrix} B_1 & B_2 & \dots & B_p \end{bmatrix} = \begin{bmatrix} (A_1 \cdot B_1) & (A_1 \cdot B_2) & \dots & (A_1 \cdot B_p) \\ (A_2 \cdot B_1) & (A_2 \cdot B_2) & \dots & (A_2 \cdot B_p) \\ \vdots & \vdots & \ddots & \vdots \\ (A_m \cdot B_1) & (A_m \cdot B_2) & \dots & (A_m \cdot B_p) \end{bmatrix}.$

This is an outer product where the product inside is replaced with the inner product. In general, block matrix multiplication works exactly like ordinary matrix multiplication, but the real product inside is replaced with the matrix product.

An alternative method results when the decomposition is done the other way around, i.e. the first factor, A, is decomposed into column vectors and the second factor, B, is decomposed into row vectors:

${AB} = \begin{bmatrix} A_1 & A_2 & \cdots & A_n \end{bmatrix} \begin{bmatrix} B_1 \\ B_2 \\ \vdots \\ B_n\end{bmatrix} = A_1 \otimes B_1 + A_2 \otimes B_2 + \cdots + A_n \otimes B_n.$

This method emphasizes the effect of individual column/row pairs on the result, which is a useful point of view with e.g. covariance matrices, where each such pair corresponds to the effect of a single sample point. An example for a small matrix:

$\begin{bmatrix} {\color{Red}1} & {\color{ForestGreen}2} & {\color{Blue}3} \\ {\color{Red}4} & {\color{ForestGreen}5} & {\color{Blue}6} \\ {\color{Red}7} & {\color{ForestGreen}8} & {\color{Blue}9} \\ \end{bmatrix} \begin{bmatrix} {\color{Red}a} & {\color{Red}d} \\ {\color{ForestGreen}b} & {\color{ForestGreen}e} \\ {\color{Blue}c} & {\color{Blue}f} \\ \end{bmatrix} = \begin{bmatrix} {\color{Red}1a} & {\color{Red}1d} \\ {\color{Red}4a} & {\color{Red}4d} \\ {\color{Red}7a} & {\color{Red}7d} \\ \end{bmatrix}+ \begin{bmatrix} {\color{ForestGreen}2b} & {\color{ForestGreen}2e} \\ {\color{ForestGreen}5b} & {\color{ForestGreen}5e} \\ {\color{ForestGreen}8b} & {\color{ForestGreen}8e} \\ \end{bmatrix}+ \begin{bmatrix} {\color{Blue}3c} & {\color{Blue}3f} \\ {\color{Blue}6c} & {\color{Blue}6f} \\ {\color{Blue}9c} & {\color{Blue}9f} \\ \end{bmatrix}.$

One more description of the matrix product may be obtained in the case when the second factor, B, is decomposed into the columns and the first factor, A, is viewed as a whole. Then A acts on the columns of B. If x is a vector and A is decomposed into columns, then

${A}x = A_1x_1+A_2x_2+\cdots+A_nx_n$ .

Algorithms for efficient matrix multiplication

The running time of square matrix multiplication, if carried out naively, is 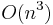$O( n^3 )$ . The running time for multiplying rectangular matrices (one m×p-matrix with one p×n-matrix) is O(mnp). But more efficient algorithms do exist. Strassen's algorithm, devised by Volker Strassen in 1969 and often referred to as "fast matrix multiplication", is based on a clever way of multiplying two 2 × 2 matrices which requires only 7 multiplications (instead of the usual 8), at the expense of several additional addition and subtraction operations. Applying this trick recursively gives an algorithm with a multiplicative cost of $O( n^{\log_{2}7}) \approx O(n^{2.807})$ . Strassen's algorithm is awkward to implement, compared to the naive algorithm, and it lacks numerical stability. Nevertheless, it is beginning to appear in libraries such as BLAS, where it is computationally interesting for matrices with dimensions n > 100^[1], and is very useful for large matrices over exact domains such as finite fields, where numerical stability is not an issue.

The currently 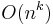$O( n^k )$ algorithm with the lowest known exponent k is the Coppersmith–Winograd algorithm. It was presented by Don Coppersmith and Shmuel Winograd in 1990, has an asymptotic complexity of O(n^2.376). It is similar to Strassen's algorithm: a clever way is devised for multiplying two k × k matrices with fewer than k³ multiplications, and this technique is applied recursively. However, the constant coefficient hidden by the Big O Notation is so large that the Coppersmith–Winograd algorithm is only worthwhile for matrices that are too large to handle on present-day computers.^[2]

Since any algorithm for multiplying two n × n matrices has to process all 2 × n² entries, there is an asymptotic lower bound of 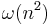$\omega (n^2)$ operations. Raz (2002) proves a lower bound of 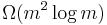$\Omega(m^2 \log m)$ for bounded coefficient arithmetic circuits over the real or complex numbers.

Cohn et al. (2003, 2005) put methods, such as the Strassen and Coppersmith–Winograd algorithms, in an entirely different group-theoretic context. They show that if families of wreath products of Abelian with symmetric groups satisfying certain conditions exist, then there are matrix multiplication algorithms with essential quadratic complexity. Most researchers believe that this is indeed the case^[3] - a lengthy attempt at proving this was undertaken by the late Jim Eve.^[4]

Because of the nature of matrix operations and the layout of matrices in memory, it is typically possible to gain substantial performance gains through use of parallelisation and vectorization. It should therefore be noted that some lower time-complexity algorithms on paper may have indirect time complexity costs on real machines.

Scalar multiplication

The scalar multiplication of a matrix A = (a_ij) and a scalar r gives a product r A of the same size as A. The entries of r A are given by

$(r\mathbf{A})_{ij} = r \cdot a_{ij}. \,$

For example, if

$\mathbf{A}=\begin{bmatrix} a & b \\ c & d \end{bmatrix}$

then

$r \cdot \mathbf{A}=\begin{bmatrix} r \cdot a & r \cdot b \\ r \cdot c & r \cdot d \end{bmatrix}$

If we are concerned with matrices over a more general ring, then the above multiplication is the left multiplication of the matrix A with scalar p while the right multiplication is defined to be

$(\mathbf{A}r)_{ij} = a_{ij} \cdot r. \,$

When the underlying ring is commutative, for example, the real or complex number field, the two multiplications are the same. However, if the ring is not commutative, such as the quaternions, they may be different. For example

$i\begin{bmatrix} i & 0 \\ 0 & j \\ \end{bmatrix} = \begin{bmatrix} -1 & 0 \\ 0 & k \\ \end{bmatrix} \ne \begin{bmatrix} -1 & 0 \\ 0 & -k \\ \end{bmatrix} = \begin{bmatrix} i & 0 \\ 0 & j \\ \end{bmatrix}i.$

Hadamard product

For two matrices of the same dimensions, we have the Hadamard product (named after French mathematician Jacques Hadamard), also known as the entrywise product and the Schur product.^[5]

Formally, for two matrices of the same dimensions:

$A, B \in {\mathbb R}^{m \times n}$

the Hadamard product A · B is a matrix of the same dimensions

$A \circ B \in {\mathbb R}^{m \times n}$

with elements given by

$(A \circ B)_{i,j} = A_{i,j} \cdot B_{i,j}$

Note that the Hadamard product is a principal submatrix of the Kronecker product.

The Hadamard product is commutative, and distributive over addition.

The Hadamard product of two positive-(semi)definite matrices is positive-(semi)definite^[6], and for positive-semidefinite $A$ and $B$

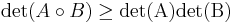$\mathrm{det}(A \circ B) \ge \mathrm{det(A)}\mathrm{det(B)}$ .

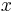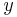For vectors $x$ and $y$ , and corresponding diagonal matrices 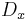$D_x$ and $D_y$ with these vectors as their leading diagonals, the following identity holds:^[7]

$x^*(A \circ B)y = \mathrm{tr}(D_x^* A D_y B^T)$ ,

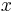where $x^*$ denotes the conjugate transpose of $x$ . In particular, using vectors of ones, this shows that the sum of all elements in the Hadamard product is the trace of $AB^T$ .

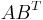A related result for square $A$ and $B$ , is that the row-sums of their Hadamard product are the diagonal elements of $AB^T:$ ^[8]

$\sum_j (A \circ B)_{i,j} = (AB^T)_{i,i}$

The Hadamard product appears in lossy compression algorithms such as JPEG.

Kronecker product

For any two arbitrary matrices A and B, we have the direct product or Kronecker product A ⊗ B defined as

$\begin{bmatrix} a_{11}B & a_{12}B & \cdots & a_{1n}B \\ \vdots & \vdots & \ddots & \vdots \\ a_{m1}B & a_{m2}B & \cdots & a_{mn}B \end{bmatrix}.$

If A is an m-by-n matrix and B is a p-by-q matrix, then their Kronecker product A ⊗ B is an mp-by-nq matrix.

The Kronecker product is not commutative.

For example

$\begin{bmatrix} 1 & 2 \\ 3 & 1 \\ \end{bmatrix} \otimes \begin{bmatrix} 0 & 3 \\ 2 & 1 \\ \end{bmatrix} = \begin{bmatrix} 1\cdot 0 & 1\cdot 3 & 2\cdot 0 & 2\cdot 3 \\ 1\cdot 2 & 1\cdot 1 & 2\cdot 2 & 2\cdot 1 \\ 3\cdot 0 & 3\cdot 3 & 1\cdot 0 & 1\cdot 3 \\ 3\cdot 2 & 3\cdot 1 & 1\cdot 2 & 1\cdot 1 \\ \end{bmatrix} = \begin{bmatrix} 0 & 3 & 0 & 6 \\ 2 & 1 & 4 & 2 \\ 0 & 9 & 0 & 3 \\ 6 & 3 & 2 & 1 \end{bmatrix}.$

If A and B represent linear transformations V₁ → W₁ and V₂ → W₂, respectively, then A ⊗ B represents the tensor product of the two maps, V₁ ⊗ V₂ → W₁ ⊗ W₂.

Frobenius inner product

The Frobenius inner product, sometimes denoted A:B is the component-wise inner product of two matrices as though they are vectors. In other words, it is the sum of the entries of the Hadamard product, that is,

$\mathbf{A}:\mathbf{B}=\sum_i\sum_j A_{ij} B_{ij} = \operatorname{trace}(\mathbf{A}^T \mathbf{B}) = \operatorname{trace}(\mathbf{A} \mathbf{B}^T).$

This inner product induces the Frobenius norm.

Powers of matrices

Square matrices can be multiplied by themselves repeatedly in the same way that ordinary numbers can. This repeated multiplication can be described as a power of the matrix. Using the ordinary notion of matrix multiplication, the following identities hold for an n-by-n matrix A, a positive integer k, and a scalar c:

$\mathbf{A}^{0} = \mathbf{I}$

$\mathbf{A}^{k} = \prod_{i=1}^k \mathbf{A}$

$\ ( c\mathbf{A} )^k = c^k\mathbf{A}^k$

$\ \text{det} (A^k) = \text{det}(A)^k.$

The naive computation of matrix powers is to multiply k times the matrix A to the result, starting with the identity matrix just like the scalar case. This can be improved using the binary representation of k, a method commonly used to scalars. An even better method is to use the eigenvalue decomposition of A.

Calculating high powers of matrices can be very time-consuming, but the complexity of the calculation can be dramatically decreased by using the Cayley-Hamilton theorem, which takes advantage of an identity found using the matrices' characteristic polynomial and gives a much more effective equation for A^k, which instead raises a scalar to the required power, rather than a matrix.

Powers of diagonal matrices

The power, k, of a diagonal matrix A, is the diagonal matrix whose diagonal entries are the k powers of the original matrix A.

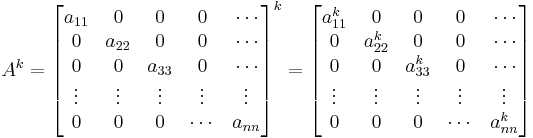
$A^k = \begin{bmatrix} a_{11} & 0 & 0 & 0 & \cdots \\ 0 & a_{22} & 0 & 0 & \cdots \\ 0 & 0 & a_{33} & 0 & \cdots \\ \vdots & \vdots & \vdots & \vdots & \vdots \\ 0 & 0 & 0 & \cdots & a_{nn} \end{bmatrix}^k = \begin{bmatrix} a_{11}^k & 0 & 0 & 0 & \cdots \\ 0 & a_{22}^k & 0 & 0 & \cdots \\ 0 & 0 & a_{33}^k & 0 & \cdots \\ \vdots & \vdots & \vdots & \vdots & \vdots \\ 0 & 0 & 0 & \cdots & a_{nn}^k \end{bmatrix}$

When raising an arbitrary matrix (not necessarily a diagonal matrix) to a power, it is often helpful to diagonalize the matrix first.

Notes

↑ Press 2007, p. 108.
↑ Robinson, Sara (2005), "Toward an Optimal Algorithm for Matrix Multiplication", SIAM News 38 (9), http://www.siam.org/pdf/news/174.pdf
↑ Robinson, 2005.
↑ Eve, 2009.
↑ (Horn & Johnson 1985, Ch. 5).
↑ (Styan 1973)
↑ (Horn & Johnson 1991)
↑ (Styan 1973)

References

Henry Cohn, Robert Kleinberg, Balazs Szegedy, and Chris Umans. Group-theoretic Algorithms for Matrix Multiplication. arXiv:math.GR/0511460. Proceedings of the 46th Annual Symposium on Foundations of Computer Science, 23-25 October 2005, Pittsburgh, PA, IEEE Computer Society, pp. 379–388.
Henry Cohn, Chris Umans. A Group-theoretic Approach to Fast Matrix Multiplication. arXiv:math.GR/0307321. Proceedings of the 44th Annual IEEE Symposium on Foundations of Computer Science, 11-14 October 2003, Cambridge, MA, IEEE Computer Society, pp. 438–449.
Coppersmith, D., Winograd S., Matrix multiplication via arithmetic progressions, J. Symbolic Comput. 9, p. 251-280, 1990.
Eve, James. On O(n^2 log n) algorithms for n x n matrix operations. Technical Report No. 1169, School of Computing Science, Newcastle University, August 2009. PDF
Horn, Roger A.; Johnson, Charles R. (1985), Matrix Analysis, Cambridge University Press, ISBN 978-0-521-38632-6
Horn, Roger A.; Johnson, Charles R. (1991), Topics in Matrix Analysis, Cambridge University Press, ISBN 978-0-521-46713-1
Knuth, D.E., The Art of Computer Programming Volume 2: Seminumerical Algorithms. Addison-Wesley Professional; 3 edition (November 14, 1997). ISBN 978-0201896848. pp. 501.
Press, William H.; Flannery, Brian P.; Teukolsky, Saul A.; Vetterling, William T. (2007), Numerical Recipes: The Art of Scientific Computing (3rd ed.), Cambridge University Press, ISBN 978-0-521-88068-8 .
Ran Raz. On the complexity of matrix product. In Proceedings of the thirty-fourth annual ACM symposium on Theory of computing. ACM Press, 2002. doi:10.1145/509907.509932.
Robinson, Sara, Toward an Optimal Algorithm for Matrix Multiplication, SIAM News 38(9), November 2005. PDF
Strassen, Volker, Gaussian Elimination is not Optimal, Numer. Math. 13, p. 354-356, 1969.
Styan, George P. H. (1973), "Hadamard Products and Multivariate Statistical Analysis", Linear Algebra and its Applications 6: 217-240

External links

The Simultaneous Triple Product Property and Group-theoretic Results for the Exponent of Matrix Multiplication
WIMS Online Matrix Multiplier
Matrix Multiplication Problems
Block Matrix Multiplication Problems
Matrix Multiplication in C
Linear algebra: matrix operations Multiply or add matrices of a type and with coefficients you choose and see how the result was computed.
Visual Matrix Multiplication An interactive app for learning matrix multiplication.